結構的振動分析將涉及到模態分析(modal analysis)、瞬態動力學分析(transient dynamics analysis)、簡諧響應分析(harmonic response analysis)、隨機譜分析(spectrum analysis) 等方面,其中結構的模態分析(固有頻率與振型)將是所有振動分析的基礎,下面將就結構的模態分析進行闡述。
結構振動分析的基本方程
描述結構動力學特征的基本力學變量和方程與靜力問題類似,但增加了慣性力項和阻尼力項,且所有的變量都將隨時間而變化。
結構振動的三大變量
- 位移:u(ξ,t),v(ξ,t)
- 應變:εx(ξ,t),εy(ξ,t),γxy(ξ,t)
- 應力:σx(ξ,t),σy(ξ,t),τ(ξ,t) 是坐標位置ξ(x,y,z) 和時間t 的函數。
結構振動的三大類方程及邊界/初始條件
1. 平衡方程(考慮慣性力和阻尼力)
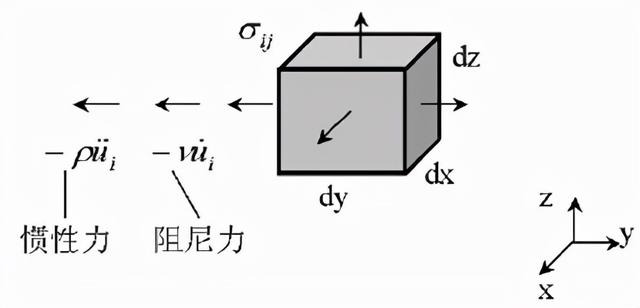

2. 幾何方程

3. 物理方程

4. 邊界/初始條件BC/IC
- 位移邊界條件BC(u)

- 力邊界條件BC(p)

- 初始條件IC(initial condition)


結構振動的有限元分析列式
用于動力學問題分析的單元構造與靜力問題相同,不同之處是所有基于節點的基本力學變量也都是時間的函數。
單元的節點位移列陣為

單元內的位移插值函數為

其中,N(ξ) 為單元的形狀函數矩陣,與相對應的靜力問題單元的形狀函數矩陣完全相同,ξ 為單元中的幾何位置坐標。
基于上面的幾何方程和物理方程以及上式,將相關的物理量(應變和應力)表達為節點位移的關系,有

單元有限元方程





將單元的各個矩陣進行組裝,可形成系統的整體有限元方程,即


1. 靜力學情形 (static case)
由于與時間無關,則

退化為

2. 無阻尼情形 (undamped system)
此時v=0,則方程

退化為

3. 無阻尼自由振動情形 (free vibration of undamped system)
則v=0,Pt=0,方程

退化為

其振動形式叫做自由振動 (free vibration),該方程解的形式為

這是簡諧振動的形式,其中ω 為常數。將其代入

有


上式有非零解的條件是

這就是特征方程(eigen equation),ω為自然圓頻率(natural circular frequency)(rad/sec),也叫圓頻率,對應的頻率為f=ω/2π(Hz)。求得自然圓頻率ω 后,再將其代入方程

可求出對應的特征向量 (eigen vector)?q ,這就是對應于振動頻率ω 的振型 (mode)。
常用單元的質量矩陣



結構振動分析將涉及到結構的剛度矩陣、質量矩陣和阻尼矩陣,由

可知,動力學問題中的剛度矩陣與靜力問題的剛度矩陣完全相同,而質量矩陣則通過下式來進行計算

對于一種單元,只要得到它的形狀函數矩陣,就可以容易地計算出質量矩陣。由阻尼矩陣的計算公式

可知,它的計算與質量矩陣相同,只是有關的系數不同而已。下面給出常見單元的質量矩陣。
桿單元的質量矩陣
質量矩陣分為兩種,即一致質量矩陣和集中質量矩陣。
1. 一致質量矩陣
對于二節點桿單元,在局部坐標內有節點位移列陣和形狀函數矩陣

相應的質量矩陣為

所謂一致質量矩陣 (consistent mass matrix) 是指,推導質量矩陣時與推導剛度矩陣時所使用的形狀函數矩陣相“一致”。
2. 集中質量矩陣
將該二節點桿單元的質量直接對半平分,集中到二個節點上,就可以得到集中質量矩陣 (lumped mass matrix)為

可以看出,集中質量矩陣的系數都集中在矩陣的對角線上,也就是說對應于各個自由度的質量系數相互獨立,相互之間無耦合;而一致質量矩陣的系數則有相互耦合。
平面三節點三角形單元的質量矩陣
1. 一致質量矩陣

2. 集中質量矩陣

來源:節選自《有限元分析及應用》,作者:曾攀 清華大學
,本文鏈接:http://www.bbbearmall.com/news-521542.html結構振動的有限元分析基礎(結構振動的有限元分析基礎)



































