陶哲軒和趙宇飛的學生聯手,給數學界整了個新驚喜:
讓組合數學領域大難題之一——從無序中證明有序,取得了23年來的重大突破。

這個問題有多難?
用知名華裔數學家、MIT副教授趙宇飛本人的話說,是“我不會建議任何學生去做這個課題”。

有意思的是,這甚至還是個“意外”收獲:
陶哲軒弟子、剛上研究生二年級的James Leng(以下簡稱小冷)原本試圖延續另一位菲爾茲獎得主——蒂莫西·高爾斯的理論研究。
但搞了一年多,他幾乎是“一無所獲”。
就在一籌莫展之時,他遇上了趙宇飛的兩位天才學生——本科期間就聯手發了十幾篇論文的Ashwin Sah(以下簡稱小薩)和Mehtaab Sawhney(以下簡稱索哥)。
三人一碰頭,頓時靈光乍現:小冷這研究思路用到塞邁雷迪定理上,那說不定真能整出點新進展。
幾個月后,都還在攻讀博士學位的三個年輕人真的做到了——
23年首次突破組合數學難題
小冷、小薩和索哥的這項研究,是組合數學領域的一大難題,是對塞邁雷迪定理的進一步研究。
塞邁雷迪定理由2012年阿貝爾獎得主、匈牙利數學家塞邁雷迪·安德烈(Szemerédi Endre,注:匈牙利人的習慣是姓前名后)于1975年證明,其中說到:
若一個整數集A具有正的自然密度,則對任意的正整數k,都可以在A中找出一個包含k項的等差數列。
所謂具有正自然密度,就是當n趨于無窮時,A與1,2,…,n這個數列的交集中元素個數與n的比值大于0。
比較著名的反例就是2,4,8…這樣的等比數列,它們被認為在數軸上“過于稀疏”,不具備正自然數密度。
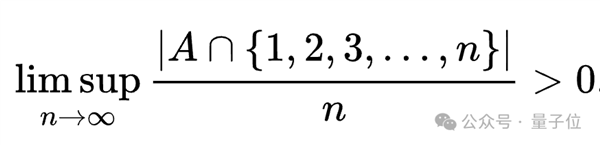
這個理論的猜想由兩名匈牙利數學家埃爾德什·帕爾(Erd?s Pál)和圖蘭·帕爾(Turán Pál)在1936年提出。
顯然對于k=1和2的情況,這個結論毫無疑問是成立的,k=3的情況則在1953年由英國數學家克勞斯·羅特證明。
到了1969年,塞邁雷迪用組合數學方法證明了k=4的情況,直到終證明該結論對任意k均成立。

后來,又有數學家利用遍歷理論、傅里葉分析等其他方法證明了這一結論。
這也讓陶哲軒為之感慨,還把該定理的眾多證明稱為“羅塞塔石碑”,因為它們連結了幾個乍看起來完全不同的數學分支。
但總之,塞邁雷迪定理的證明并不是一個終點,而且還開啟了新的討論。
塞邁雷迪定理還有另一種表述形式——
若在正整數1-N中取一個子集,使得對于某一k值,在該子集中找不到長度為k的等差數列;
則當N趨近于無窮時,該子集的大小r_k(N)與N的比值趨近于0。
不過這個比值趨近于0的速度究竟是怎樣的,仍然是一個未知數,也就成了后續這幾十年的研究課題。
前面提到,有人用傅里葉分析方法給出了塞邁雷迪定理的新證明,這個人就是1998年菲爾茲獎得主、英國數學家蒂莫西·高爾斯(Timothy Gowers)。

更重要的是,高爾斯同時給出了r_k(N)與N比值的上界,即該比值下降的速度不會慢于某個特定的函數。
這個函數長這樣:
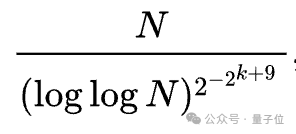
此后的20多年來,不斷有人針對具體k值,對r(N)的范圍給出了更精確的上界。
比如在2017年,陶哲軒和英國數學家本·格林(Ben Green)一起給出了k=4時的新上界。

然而,對k取任意值的情況一直未有新的進展,直到這次研究的出現。
2022年,正在加州大學洛杉磯分校(UCLA)讀研二的小冷開始研究起了高爾斯的理論。
不過他腦海里的是高爾斯提出的幾個技術問題,并沒有想到塞邁雷迪定理。
一年很快過去,小冷沒有得到任何成果,但他的研究引起了小薩和索哥的注意。
他們意識到,小冷的研究可能有助于在塞邁雷迪定理上取得進一步進展。
于是三位年輕的數學家走到了一起,并在幾個月之內就想出了k=5時更精確的上界。

直到今年,三人又把這一結論推廣到了k為任意取值的情況,成為了23年以來在這個問題上重大的突破。
證明的核心在于應用了高爾斯U^(k+1)范數的逆定理,這是一個與傅里葉分析相關的高級工具,它提供了一種衡量函數在某種意義上接近于零的方法。
該逆定理也是由三人發現的,用了足足100頁的論文進行闡述。
其中指出,如果一個函數在范數意義上足夠大,那么它必然與某些具有特定結構的序列相關聯,這些序列在數學上被稱為“結構性對象”。

利用這個逆定理,作者們將問題從原始的整數集合,轉移到了具有特定代數結構的nilmanifolds流形上。
通過深入分析這些流形上的nil序列,作者們實現了對這些序列在整數集合上變化的控制。
然后,他們通過對集合進行分解并運用密度增量策略,逐步增加不包含k項等差數列的子集密度,直到達到某一閾值或無法繼續增加。
經過迭代這個過程,作者們證明了存在一個足夠大的子集,其密度遠高于之前的結果,實現了k=5時結論向著更高k值的推廣。
陶哲軒趙宇飛的天才學生們
三位作者中,小冷(James Leng)目前就讀于加州大學洛杉磯分校(UCLA),師從菲爾茲獎得主陶哲軒。
他的主要研究方向是算術組合學、動力系統和傅里葉分析。

而小薩(Ashwin Sah)和索哥(Mehtaab Sawhney)都是MIT副教授趙宇飛的學生。
小薩其人,不可謂不是一位“天才少年”。
他是2016年國際奧林匹克數學競賽(IMO)金牌得主,2018年還獲得過首屆阿里巴巴全球數學競賽銀獎。
剛上大一,小薩就跑去聽了趙宇飛研究生級別的組合數學課。這迅速引起了趙宇飛的注意:
盡管他只是大一的學生,但很顯然,他已經掌握了這門課程。

就在本科期間,小薩已經有20多篇數學論文在手——并且他只用了兩年半時間就從MIT本科畢業了。
其中,還包括在拉姆齊數方面的重大突破:給出了拉姆齊數的新上限,被認為是“使用現有研究線索可以獲得的佳結果”。
索哥(Mehtaab Sawhney)比小薩高一年級,他同樣在本科期間就參與了趙宇飛的組合數學課程。

打從本科起,索哥和小薩就是彼此的科研搭子,關系密切到索哥主頁列出的70篇論文里,有60篇都帶小薩的名字。
而導師趙宇飛在本科時對他倆的評價就是:
(MIT)的本科生研究有著悠久的歷史和傳統,但在論文的質量和數量上,都達不到Ashwin Sah和Mehtaab Sawhney的水平。
目前,索哥已經率先博士畢業,獲得了哥倫比亞大學的教職,還在今年年初被任命為克萊研究員。

△小薩索哥和趙宇飛合影,圖源:MIT
兩位老友的合作仍在繼續,這也令外界感到期待。他們的導師趙宇飛是這樣說的:
他們的非凡之處在于總能理解極具技術挑戰的事物并加以改進。
很難用語言概括他們的整體成就。
參考鏈接:
[1]https://arxiv.org/abs/2402.17995
[2]https://www.quantamagazine.org/grad-students-find-inevitable-patterns-in-big-sets-of-numbers-20240805/
[3]https://en.wikipedia.org/wiki/Szemer%C3%A9di%27s_theorem
本文鏈接:http://www.bbbearmall.com/news-131267.html數學難題被攻下 23年來首次突破